LeetCode每日一题2023-12

学习笔记 评论

2023.12LeetCode每日一题

2023.12.11 最小体力消耗路径[中等]

1631. 最小体力消耗路径

思路:

  1. 深搜\宽搜:统计所有路径，然后找到最小的路径
  2. 动态规划:dp[i][j]表示到达i,j的最小消耗，dp[i][j]=min(dp[i-1][j],dp[i][j-1])+abs(heights[i][j]-heights[i-1][j-1])

错误: 题目求的不是最小消耗的路径,而是这个路径上最大绝对值差值的最小()

题解:

  1. 二分:二分的是最大绝对值差值,然后判断是否能够到达终点(深搜宽搜),能到就继续缩小差值,不能就增大差值
  2. 并查集:将所有边按照权值从小到大排序,然后依次加入并查集,如果起点和终点连通,那么这个权值就是答案
  3. 最短路径算法:当前最短路径可以表示为这条路径上最大的权重(普通的最短路径应该表示为这条路径上权重的和),然后使用最短路径算法求解

2023.12.12 😒用邮票贴满网格图[困难]

2132. 用邮票贴满网格图

2023.12.13 下一个更大元素 IV[困难]

下一个更大元素 I[简单]

  1. 先在nums2中找到当前元素的位置,然后从这个位置开始遍历,找到第一个比当前元素大的元素,如果找不到就返回-1
  2. 单调栈+Hash表,先对nums2进行单调栈处理(从后往前记录(相当于当前元素和他左边的元素无关),从栈底到栈顶递增),然后用一个map记录每个数字对应的右边第一个比它大的数字,最后遍历nums1,直接从map中取值

下一个更大元素 II[中等]

  1. 单调栈+循环数组,循环数组使用取余的方式实现, 单调栈里存的是数组下标(元素从栈底到栈顶递减),当栈顶的元素被弹出来时,说明当前元素是栈顶元素右边第一个比它大的元素,栈顶元素的答案就是遍历到的当前元素

下一个更大元素 III[中等]

  1. 分析＋单调栈,对一个数字:564973,从后往前找(因为是最小的,动后面的肯定最小)
  • 对于3,后面没有比它大的数字,所以3不动
  • 对于73,没有比7大的数字,所以不动
  • 对于973,没有比9大的数字,所以不动
  • 对于4973,找到后面比4大的最小的数字,交换4和7,得到567,在对剩下的数字排序,得到349,答案就是567349
  1. 类似31.下一个排列
  • [31.下一个排列],从后往前先找到第一个正序对,然后再从后往前找到第一个比这个正序对中的第一个数字大的数字,交换这两个数字,然后将后面的数字排序
  • [31.下一个排列]也可以用1的方法做

下一个更大元素 IV[困难]

  1. 用一个最小堆q来存储已经找到下一个比他大的元素,用一个单调栈st来存储还没找到下一个比他大的元素的元素,具体操作:
    • 如果q非空,且堆顶元素小于栈顶元素,说明堆顶的这个元素找到了第二个比他大的元素,重复操作直到堆顶元素大于栈顶元素或者堆为空
    • 如果st非空,且栈顶元素小于当前元素,说明栈顶元素找到了第一个比他大的元素,将栈顶元素弹出加入到堆中,重复操作直到栈顶元素大于当前元素或者栈为空
    • 将当前元素入栈
  2. 最小堆复杂度是O(nlogn)O(nlogn),使用单调栈替换掉最小堆,复杂度就是O(n)O(n)
    • 用一个stack2代替最小堆,只要保证stack2是一个从栈底到栈顶单调递减的栈,如何保证stack2是单调递减的:从1可知堆顶的元素一定是大于栈里的,因此在stack1弹出来的时候,不要一个个弹,用切片弹,然后把整个切片加入到stack2中,这样就保证了stack2是单调递减的

2023.12.13 字典序最小回文串[简单]

2697. 字典序最小回文串

思路:

  1. 从左开始遍历到字符串长度的中间,如果遇到不相等的字符,那么就将这两个字符替换为二者之间最小的(双指针)

2023.12.15 反转二叉树的奇数层[中等]

2415. 反转二叉树的奇数层

思路:

  1. 宽搜,难点在于如何存储每一层的节点,想法是用两个队列,一个从左往右搜左子树的,一个从右往左搜右子树的,这样顺序就是对称的.到奇数层直接交换两个队列的当前节点的值就行
  2. 想复杂了,只要交换值就行,不用交换节点

题解:

  1. 宽搜,把每一层的节点都存到list里,奇数层交换
  2. 深搜, 传递两个节点,一个从最左边往下搜, 一个从最右边往下搜,奇数层则交换这两个节点的值

2023.12.16 统计区间中的整数数目[苦难]

2276. 统计区间中的整数数目

线段树解决的是「区间和」问题，并且该「区间」会被修改。

线段树最简单模板

思想:将数组看成一棵树,叶子节点是数组的值,非叶子节点代表了其叶子节点区间的和/最大值/最小值.
307. 区域和检索 - 数组可修改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
class SegTreeSimple:
  def __init__(self, nums):
    self.tree = [0] * (4 * len(nums))
    self.nums=nums
    self.build(1,0,len(nums)-1)

  def build(self, cur, left, right):
    '''
    l,r表示的是当前需要构建的区间
    cur是[l,r]区间的在树中的节点
    l==r说明到达了树的叶子节点,那么cur的值就是数组的值
    '''
    # 到达当前节点
    if left==right:
      self.tree[cur] = self.nums[left]
      return
    mid = (left + right) // 2
    #　构建左右子树
    self.build(cur * 2, left, mid)
    self.build(cur * 2 + 1, mid + 1, right)
    # 向上更新
    self.pushup(cur)

  def pushup(self, root):
    # 求区间   和/最大值/最小值
    self.tree[root] = self.tree[root * 2] + self.tree[root * 2 + 1]

  # 区间更新
  def updateArrange(self, cur, left, right, start, end , val):
    '''
    cur是当前在数中的节点
    l,r是要更新的区间
    start,end是当前区间
    val是要更新的值
    '''
    if start == end:
        self.tree[cur] = val
        return
    if left<start or right>end:
        return 
    mid = (start + end) // 2
    if left <= mid:
        self.updateArrange(cur * 2, left, right, start, mid, val)
    if right>mid:
        self.updateArrange(cur * 2 + 1, left, right, mid+1, end, val)
    self.pushup(cur)

  # 单点更新
  def update(self, cur, left, right, index, val):
    '''
    cur是当前区间在树中的节点
    l,r是要更新的数组的区间
    index是要更新的数组的索引
    val是要更新的值
    '''
    if left == right:
      # 覆盖式,也可是增量式
      self.tree[cur] = val
      return
    mid = (left + right) // 2
    if index <= mid:
      self.update(cur * 2, left, mid, index, val)
    else:
      self.update(cur * 2 + 1, mid + 1, right, index, val)
    self.pushup(cur)
  
  # 区间查询
  def query(self, cur, left, right, start, end):
    '''
    left,right是要查询的区间
    cur是当前区间对应的树的节点
    start,end是当前区间
    '''
    # 当前区间完全处于查询区间之内
    if left <= start and end <= right:
      return self.tree[cur]
    mid = (start + end) // 2
    ans = 0
    if left <= mid:
      ans += self.query(cur * 2, left, right, start, mid)
    if right > mid:
      ans += self.query(cur * 2 + 1, left, right, mid + 1, end)
    return ans

线段树Lazy模板

思想:
在上面查询的时候,如果当前区间包括在查询区间里面,那么就可以直接返回当前区间的值而不用向下传递.
在区间修改时,如果当前区间包括在修改区间里面,那么也可以直接修改当前区间的值而不用向下传递(如果向下传递的话相当于遍历其子树时间复杂度为O(n)O(n)).
做法是使用一个lazy数组记录当前区间需要向下传递的值,在查询,如果当前区间需要向下传递的值不为0,那么就向下传递,并且将当前区间的lazy值清零

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
class SegTreeLazy:
  def __init__(self, nums):
    self.tree = [0] * (4 * len(nums))
    self.lazy = [0] * (4 * len(nums))
    self.nums=nums
    self.build(1,0,len(nums)-1)

  def build(self, cur, left, right):
    '''
    l,r表示的是当前需要构建的区间
    cur是[l,r]区间的在树中的节点
    l==r说明到达了树的叶子节点,那么cur的值就是数组的值
    '''
    # 到达当前节点
    if left==right:
      self.tree[cur] = self.nums[left]
      return
    mid = (left + right) // 2
    #　构建左右子树
    self.build(cur * 2, left, mid)
    self.build(cur * 2 + 1, mid + 1, right)
    # 向上更新
    self.pushup(cur)

  def pushup(self, root):
    # 求区间   和/最大值/最小值
    self.tree[root] = self.tree[root * 2] + self.tree[root * 2 + 1]

  # 单点更新
  def update(self, cur, left, right, index, val):
    '''
    cur是当前区间在树中的节点
    l,r是要更新的数组的区间
    index是要更新的数组的索引
    val是要更新的值
    '''
    if left == right:
      # 覆盖式,也可是增量式
      self.tree[cur] = val
      return
    mid = (left + right) // 2
    if index <= mid:
      self.update(cur * 2, left, mid, index, val)
    else:
      self.update(cur * 2 + 1, mid + 1, right, index, val)
    self.pushup(cur)

    # 区间更新
  def updateRange(self, cur, left, right, start, end, val):
    # 当前区间完全处于查询区间之内
    if left <= start and end <= right:
      # 只更新当前区间的值,不向下传递
      self.tree[cur] += val * (end - start + 1)
      # 记录当前区间需要向下传递的值,如果不是区间没必要向下传递
      if start != end:
        self.lazy[cur] += val
      return
    mid = (start + end) // 2
    # 向下传递lazy值,如果是覆盖式更新,不能使用self.lazy!-0判断,需要使用额外的bool数组
    if self.lazy[cur] != 0:
      self.pushdown(cur, start, end, mid)
    if left <= mid:
      self.updateRange(cur * 2, left, right, start, mid, val)
    if right > mid:
      self.updateRange(cur * 2 + 1, left, right, mid + 1, end, val)
    self.pushup(cur)
  
  def pushdown(self, cur, start, end, mid):
    # 向下传递lazy值,值传递到子节点
    self.tree[cur * 2] += self.lazy[cur] * (mid - start + 1)
    self.tree[cur * 2 + 1] += self.lazy[cur] * (end - mid)
    self.lazy[cur * 2] += self.lazy[cur]
    self.lazy[cur * 2 + 1] += self.lazy[cur]
    self.lazy[cur] = 0
  
  # 区间查询
  def query(self, cur, left, right, start, end):
    '''
    left,right是要查询的区间
    cur是当前区间对应的树的节点
    start,end是当前区间
    '''
    # 当前区间完全处于查询区间之内
    if left <= start and end <= right:
      return self.tree[cur]
    mid = (start + end) // 2
    ans = 0
    if self.lazy[cur] != 0:
       self.pushdown(cur, start, end, mid)
    if left <= mid:
      ans += self.query(cur * 2, left, right, start, mid)
    if right > mid:
      ans += self.query(cur * 2 + 1, left, right, mid + 1, end)
    return ans

线段树离散化模板


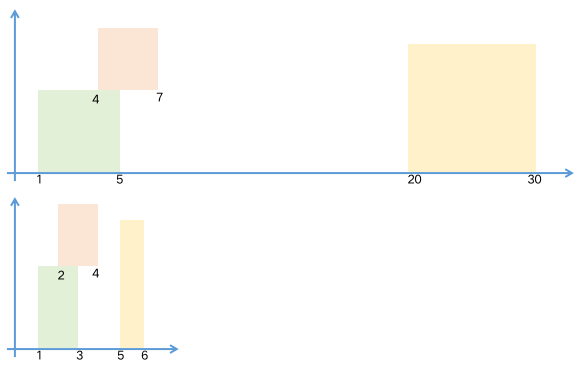
思想:
需要直到全部的区间坐标
做好原数组与离散后数组的映射关系
699. 掉落的方块

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
class SegTreeDiscrete:
  def __init__(self, n ):
    self.tree = [0] * (4 * n)
    self.lazy = [0] * (4 * n)
    self.build(1,0,n-1)

  def build(self, cur, left, right):
    if left==right:
      self.tree[cur] = 0
      return
    mid = (left + right) // 2
    self.build(cur * 2, left, mid)
    self.build(cur * 2 + 1, mid + 1, right)
    self.pushup(cur)

  def pushup(self, root):
    self.tree[root] = max(self.tree[root * 2] , self.tree[root * 2 + 1])

  def updateRange(self, cur, left, right, start, end, val):
    if left <= start and end <= right:
      self.tree[cur] = val
      if start != end:
        self.lazy[cur] = val
      return
    mid = (start + end) // 2
    if self.lazy[cur] != 0:
      self.pushdown(cur, start, end, mid)
    if left <= mid:
      self.updateRange(cur * 2, left, right, start, mid, val)
    if right > mid:
      self.updateRange(cur * 2 + 1, left, right, mid + 1, end, val)
    self.pushup(cur)
  
  def pushdown(self, cur, start, end, mid):
    self.tree[cur * 2] = self.tree[cur]
    self.tree[cur * 2 + 1] = self.tree[cur]
    self.lazy[cur * 2] = self.lazy[cur]
    self.lazy[cur * 2 + 1] = self.lazy[cur]
    self.lazy[cur] = 0
  
  def query(self, cur, left, right, start, end):
    if left <= start and end <= right:
      return self.tree[cur]
    mid = (start + end) // 2
    ans = -1
    if self.lazy[cur] != 0:
       self.pushdown(cur, start, end, mid)
    if left <= mid:
      ans = max(self.query(cur * 2, left, right, start, mid), ans)
    if right > mid:
      ans = max(self.query(cur * 2 + 1, left, right, mid + 1, end), ans)
    return ans

class Solution:
    # 离散化,原值->离散后的索引(值)
    def discrete(self,nums):
        num_set = set(nums)
        num_list = sorted(list(num_set))
        return {num: idx + 1 for idx, num in enumerate(num_list)}
    
    def fallingSquares(self, positions: List[List[int]]) -> List[int]:
        n = len(positions)
        arr = [0] * (2 * n)
        size = 0
        for i in range(n):
            arr[i * 2] = positions[i][0]
            arr[i * 2 + 1] = positions[i][0] + positions[i][1]
            size = max(size, arr[i * 2 + 1])
        arr_map = self.discrete(arr)
        st = SegTreeDiscrete(len(arr_map))
        res = []
        height = 0
        max_height = 0
        for i in range(n):
            l = arr_map[positions[i][0]]
            h = positions[i][1]
            r = arr_map[positions[i][0] + h]
            
            height = st.query(1, l, r-1 , 0, len(arr_map)-1)
            st.updateRange(1, l, r-1,0,len(arr_map)-1, height + h)

            max_height = max(max_height, height + h)
            res.append(max_height)
        return res

线段树动态开点模板

思想:
不能在程序开始时就完成初始线段树的构建，在区间查询或区间修改时，根据传入的区间信息来动态地创建结点
2276. 统计区间中的整数数目
715. Range 模块

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
class Node:
    def __init__(self):
      self.leftChild = None
      self.rightChild = None
      self.val = 0
      self.lazy = 0

class SegTreeDynamicPointer:
  def __init__(self):
    self.root = Node()

  def pushup(self, curNode):
    curNode.val=curNode.leftChild.val+curNode.rightChild.val

  def AddNode(self, curNode):
    if curNode.leftChild == None:
      curNode.leftChild = Node()
    if curNode.rightChild == None:
      curNode.rightChild = Node()

  def pushdown(self, curNode, start, end, mid):
    curNode.leftChild.val = (mid - start + 1)
    curNode.rightChild.val = (end - mid)
    curNode.leftChild.lazy = curNode.lazy
    curNode.rightChild.lazy = curNode.lazy
    curNode.lazy = 0

  # 区间更新
  def updateRange(self, curNode, left, right, start, end, val):
    # 当前区间完全处于查询区间之内
    if left <= start and end <= right:
      curNode.val = (end-start+1)
      if start != end:
        curNode.lazy = 1
      return
    # 动态开点
    self.AddNode(curNode)
    mid = (start + end) // 2
    if curNode.lazy != 0:
      self.pushdown(curNode, start, end, mid)
    if left <= mid:
      self.updateRange(curNode.leftChild, left, right, start, mid, val)
    if right > mid:
      self.updateRange(curNode.rightChild, left, right, mid + 1, end, val)
    self.pushup(curNode)
  
  # 区间查询
  def query(self, curNode, left, right, start, end):
    if left <= start and end <= right:
      return curNode.val
    self.AddNode(curNode)
    mid = (start + end) // 2
    if curNode.lazy != 0:
       self.pushdown(curNode, start, end, mid)
    ans = 0
    if left <= mid:
      ans += self.query(curNode.leftChild, left, right, start, mid)
    if right > mid:
      ans += self.query(curNode.rightChild, left, right, mid + 1, end)
    return int(ans)

class CountIntervals:
    def __init__(self):
        self.tree=SegTreeDynamicPointer()
        self.N=1e9+1
        self.node=self.tree.root
        self.max_num=0

    def add(self, left: int, right: int) -> None:
        self.max_num=max(self.max_num,right)
        self.tree.updateRange(self.node,left,right,0,self.N,1)

    def count(self) -> int:
        return self.tree.query(self.node,0,self.max_num,0,self.N)

2023.12.17 使用最小花费爬楼梯[简单]

746. 使用最小花费爬楼梯

思路:简单动态规划,第一阶和第二阶应该是0

2023.12.18 寻找峰值[中等]

162. 寻找峰值

思路:单调栈从栈底到栈顶递增,栈底元素一定大于其左边元素,同时也大于栈中其他元素,因此答案就是栈底元素

2023.12.19 寻找峰值 II[中等]

1901. 寻找峰值 II

思路:一维的峰值扩展到二维,无思路

题解:二分,使用二分分行,然后找到每一行的最大值,用这一行的最大值和他的上下两行的值比较,如果上面的大则继续二分上面的行,否则二分下面的行

2023.12.20 判别首字母缩略词[简单]

2828. 判别首字母缩略词

思路:数组里面每个单次的首字符看看能不能组成这个单词,先判断两个长度是不是一样

2023.12.21 美丽塔 II[中等]

思路:暴力,两重循环,判断每个点的左右两边是否满足条件,但是肯定超时

题解:先预处理每个点左右两边,左边为例,用单调栈(从栈底到栈顶递增,存下标),如果当前元素比栈顶元素小,那么就弹出栈顶元素,直到栈顶元素大于当前元素,那么栈顶元素到当前元素之间的元素都是比当前元素大的,这区间只能选择当前元素的高度,然后再加上栈顶元素左边的高度和,得到了当前元素左边的高度和,右边的高度和同理,然后再遍历每个点,每个点的答案就是左边的高度和+右边的高度和-当前点的高度

1
2
3
4
5
# 预处理代码
prefix[i]=(long)(i-left.Peek())*maxHeights[i]+prefix[left.Peek()];
suffix[i]=(long)(right.Peek()-i)*maxHeights[i]+suffix[right.Peek()];
# 答案代码
res=Math.Max(suffix[i]-maxHeights[i]+prefix[i],res);

2023.12.22 得到山形数组的最少删除次数[困难]

最长递增子序列模板

动态规划O(N2)O(N^2)

1
2
3
4
5
6
7
8
def MaxSeqInN2(self,nums):
  n=len(nums)
  dp=[1]*(n)
  for i in range(n):
      for j in range(i):
          if nums[i]>nums[j]:
              dp[i]=max(dp[i],dp[j]+1)
  return max(dp)

长度数组O(NlogN)O(NlogN)

1
2
3
4
5
6
7
8
9
10
def MaxSeqInLogn(self,nums):
  n=len(nums)
  len2num=[float('inf')]*(n+1)
  len2num[0]=float('-inf')
  ans=-1
  for i,num in enumerate(nums):
      lengthIndex=bisect_left(len2num,num)
      len2num[lengthIndex]=num
      ans=max(ans,lengthIndex)
  return ans

得到山形数组的最少删除次数

1671. 得到山形数组的最少删除次数

思路:以为和美丽塔 II一样,但是区别在于这一题需要左边的长度越长越好,美丽塔 II有个高度

题解:预处理每个点左右两边的最长递增子序列,遍历每个点,当前点的答案就是左边的最长递增子序列+右边的最长递增子序列-1(当前点被计算了两次)

2023.12.23 移除石子使总数最小[中等]

1962. 移除石子使总数最小

思路:贪心,用优先队列(最大堆),每次取堆顶的元素然后整除2再放回堆里,重复k次

2023.12.24 收集足够苹果的最小花园周长[中等]

1954. 收集足够苹果的最小花园周长

思路:两重循环遍历(x,y)的坐标
题解:找规律,计算出如何用n表示苹果的数量,然后二分找到n>=neededApples的最小的n,然后计算出边长,公式为2n(n+1)(2n+1)2n(n+1)(2n+1).

2023.12.25 不浪费原料的汉堡制作方案[中等]

1276. 不浪费原料的汉堡制作方案

思路:小的和巨无霸都只用一个奶酪片,枚举一个的数量,另一个就是奶酪片-枚举的数量,然后判断是否满足条件
题解:二元一次方程,解方程组

2023.12.26 😒参加考试的最大学生数[困难]

1349. 参加考试的最大学生数

位运算基础

参加考试的最大学生数

2023.12.27 保龄球游戏的获胜者[简单]

2660. 保龄球游戏的获胜者

思路:模拟,重要的是代码的复用

2023.12.28 收集巧克力[中等]

2735. 收集巧克力

思路:无思路,因为对当前节点每操作一次都会对后面的节点造成影响,无头绪
题解:

  1. 最多移动n-1次,因为移动n次就没动了,所以枚举移动次数(1,n-1),那么对于每个节点,他的选择就是移动或者不移动dp[i][k]=min(dp[i][k−1],nums[(i+k)%n])dp[i][k]=min(dp[i][k-1],nums[(i+k)\%n]),答案就是当前移动次数的所有节点的总和ans=min(ans,k∗x+∑i=0n−1dp[i][k]ans=min(ans,k * x+\sum_{i=0}^{n-1}dp[i][k]
  2. 二次差分:看不懂

优化:二维dp之和k-1有关系,可以改成一维的

2023.12.29 购买两块巧克力[简单]

2706. 购买两块巧克力

2023.12.30 一周中的第几天[简单]

1185. 一周中的第几天

思路:模拟
题解:巧用语言中的库函数

2023.12.31 一年中的第几天[简单]

1154. 一年中的第几天
思路:模拟
题解:语言的类库多看看

GladdduckKB Master

我写的个人简介。