[toc]
推荐一篇写的很好的课件
多项式的表示与乘法
- 系数表示法
多项式A(x)=∑i=0naixi的系数表示就是
a=(a0,a1,...,an)T
如果用系数表示,多项式乘法的复杂度是O(n2),就是和平时手算过程一样
- 点值表示法
n+1个不同的点能唯一确定n次多项式系数
对于多项式A(x),B(x)
A(x):{(x0,y0),(x1,y1),(x2,y2),…,(xn,yn)},
B(x):{(x0,y0′),(x1,y1′),(x2,y2′),…,(xn,yn′)}
设 C(x)=A(x)B(x),因为C(x)的系数是2n,所以要在A(x)和B(x)上取2n个不同的点才行,C(x)的点值表示为
{(x0,y0y0′),(x1,y1y1′),(x2,y2y2′),…,(x2n,y2ny2n′)}
点值表示的多项式乘法复杂度为O(n)
系数表示法与点值表示法的转换
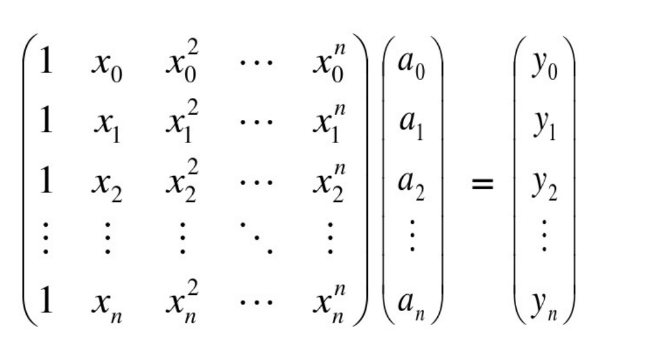
系数到点(也叫求值):Xa=y
因为系数矩阵行列式不为0,所以可逆.
点到系数(也叫插值):a=X−1y
单位复数根
n次单位复数根满足wn=1,n次单位复数根敲好有n个
复杂证明略过,n次单位根的所有根,作为计算点值的x
离散傅里叶变换
对于 n 次多项式 A(x)=∑i=0naixi ,
其系数形式为 a=(a0,a1,…,an)T .
设 $ y_{k}=A\left(\omega_{n}{k}\right)=\sum_{i=0}{n} a_{i} \omega_{n+1}^{k i}, 0 \leq k \leq n, k \in N $,
则向量 $ y=\left(y_{0}, y_{1}, \ldots, y_{n}\right)^{T} $
就是系数向量 $ a=\left(a_{0}, a_{1}, \ldots, a_{n}\right)^{T} $ 的离散傅里叶变换.
但是离散傅里叶变换的复杂度仍是O(n2)
快速傅里叶变换(FFT)
FFT 将A(x)拆分为奇数下标与偶数下标的系数
A[0](x)=a0+a2x+a4x2+⋯+an−1x2n−1,
A[1](x)=a1+a3x+a5x2+⋯+anx2n−1.
A[0](x) 包含 A 所有偶数下标的系数, $ A^{[1]}(x)$ 数下标的系数, 于是有:
A(x)=A[0](x2)+xA[1](x2).
所以, 求 $ A(x)$ 在 ωn+10,ωn+11,…,ωn+1n 处的值的问题转化为:
a. 求次数为 $ \frac{n}{2}$ 的多项式 $ A^{[0]}(x), A^{[1]}(x) $
在点 (ωn+10)2,(ωn+11)2,…,(ωn+1n)2 处的取值.
递归即可得到结果.
复杂度
T(n)=2T(2n)+Θ(n)
然后进行点值乘法,得到点值的结果,再利用逆变换为系数表达.
具体流程
- 加倍多项式次数
通过加入 n 个系数为 0 的高阶项, 把多项式 $ A(x) 和 B(x)$ 变为次数为 2n 的 多项式, 并构造其系数表达.
- 求值
通过应用 $ 2(n+1) $ 阶的 $FFT $计算出 $A(x) 和 B(x) $ 长度为 $ 2(n+1) $ 的点值表达. 这些点值表达中包含了两个多项式在 $ 2(n+1) $ 次单位根处的取值.
- 逐点相乘
把 $A(x) 的值与 B(x) $的值逐点相乘, 可以计算出 $C(x)=A(x) B(x) $ 的点值表 达, 这个表示中包含了 $ C(x) 在每个 2(n+1) $ 次单位根处的值.
- 揷值
通过对 $2(n+1) $ 个点值应用 FFT, 计算其逆 DFT, 就可以构造出多项式C(x)的系数表达
由于 $ 1 、 3 $ 的时间复杂度为 $ \Theta(n)$, $2 、 4 $ 的时间复杂度为 Θ(nlog2n) ,
因此整个算法的时间复杂度为 $ \Theta\left(n \log _{2} n\right)$ .
python 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
| import math
PI = 3.1415926
class complex:
def __init__(self,real=0,virtual=0) -> None:
self.real=real
self.virtual=virtual
def __str__(self) -> str:
return f'real:{self.real} virtual:{self.virtual}\n'
def complex_mut(a,b):
ret=complex()
ret.real = a.real * b.real - a.virtual * b.virtual
ret.virtual = a.real * b.virtual + a.virtual * b.real
return ret
def complex_add(a,b):
ret=complex()
ret.real = a.real + b.real
ret.virtual = a.virtual + b.virtual
return ret
def complex_sub(a,b):
ret=complex()
ret.real = a.real - b.real
ret.virtual = a.virtual - b.virtual
return ret
def get_w(n,k,inverse):
w=complex()
accy=round(PI*2*k/n,6)
if inverse:
w.real=round(math.cos(accy),6)
w.virtual=round(-math.sin(accy),6)
else:
w.real=round(math.cos(accy),6)
w.virtual=round(math.sin(accy),6)
return w
def FFT(coefficient,n,inverse):
if n==1:
return coefficient
odd,even=[],[]
for index in range(n):
if index&1:
odd.append(coefficient[index])
else:
even.append(coefficient[index])
e_k=FFT(even,n//2,inverse)
d_k=FFT(odd,n//2,inverse)
y_k,y_k_2=[],[]
for i in range(n//2):
w=get_w(n,i,inverse)
y_k.append(complex_add(e_k[i],complex_mut(w,d_k[i])))
y_k_2.append(complex_sub(e_k[i],complex_mut(w,d_k[i])))
return y_k+y_k_2
def polynomial_mul(coefficient_a,coefficient_b):
coefficient_a=coefficient_a[::-1]
coefficient_b=coefficient_b[::-1]
length=len(coefficient_a)-1+len(coefficient_b)-1
digitnum = 1
while length>0:
length>>=1
digitnum+=1
length = 1
while digitnum>0:
length<<=1
digitnum-=1
a,b=[complex() for _ in range(length+1)],[complex() for _ in range(length+1)]
for index,item in enumerate(coefficient_a):
a[index].real=item
for index,item in enumerate(coefficient_b):
b[index].real=item
FFT_a=FFT(a,length,inverse=False)
FFT_b=FFT(b,length,inverse=False)
c=[]
for index in range(length):
c.append(complex_mut(FFT_a[index],FFT_b[index]))
FFT_c=FFT(c,length,inverse=True)
ans=[]
for item in FFT_c:
if item.real/length>0.05 or item.real/length<-0.05:
ans.append(round(item.real/length,2))
else:
ans.append(0)
return ans
if __name__=='__main__':
a=[0,3,2]
b=[2,1,1]
c=polynomial_mul(a,b)
astr=' + '.join([f'{item}*x^{index} ' for index,item in enumerate(a[::-1])][::-1])
bstr=' + '.join([f'{item}*x^{index} ' for index,item in enumerate(b[::-1])][::-1])
print(f" {astr}")
print(f"* {bstr}")
cstr=' + '.join([f'{item}*x^{index} ' for index,item in enumerate(c) if item !=0 ][::-1] )
print(f"= {cstr}")
|
C++代码
来自知乎
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
| #include<iostream>
#include<vector>
#include<iomanip>
#include<math.h>
using namespace std;
const double PI = 3.1415926;
struct _complex{
double x;
double y;
};
_complex a[4096], b[4096];
bool is_output[4096];
_complex omega(const int& n, const int& k,bool inverse)
{
_complex r;
if (!inverse)
{
r.x = cos(PI * 2 * k / n);
r.y = sin(PI * 2 * k / n);
}
else
{
r.x = cos(PI * 2 * k / n);
r.y = -sin(PI * 2 * k / n);
}
return r;
}
inline _complex operator*(_complex a, _complex b)
{
_complex r;
r.x = a.x * b.x - a.y * b.y;
r.y = a.x * b.y + a.y * b.x;
return r;
}
inline _complex operator+(_complex a, _complex b)
{
_complex r;
r.x = a.x + b.x;
r.y = a.y + b.y;
return r;
}
inline _complex operator-(_complex a, _complex b)
{
_complex r;
r.x = a.x - b.x;
r.y = a.y - b.y;
return r;
}
void Real_DFT(_complex* a, bool inverse, int anum)
{
if (anum == 1)
return;
vector<_complex> buf1, buf2;
for (int i = 0; i < anum ; i++)
{
if (i & 1)
{
buf2.push_back(a[i]);
}
else
{
buf1.push_back(a[i]);
}
}
for (int i = 0; i < anum / 2; i++)
{
a[i] = buf1[i];
a[i + anum / 2] = buf2[i];
}
Real_DFT(a, inverse, anum / 2);
Real_DFT(a + anum / 2, inverse, anum / 2);
int armlength = anum / 2;
for (int i = 0; i < armlength; i++)
{
_complex t = omega(anum, i, inverse);
buf1[i] = a[i] + t * a[i + anum / 2];
buf2[i] = a[i] - t * a[i + anum / 2];
}
for (int i = 0; i < anum / 2; i++)
{
a[i] = buf1[i];
a[i + anum / 2] = buf2[i];
}
return;
}
int main()
{
int numa = 0, numb = 0;
cin >> numa;
int ptr0 = 0, maxa = 0, sum = 0, ptr1 = 0,maxb=0;
for (int i = 0; i<numa; i++)
{
int id = 0;
cin >> id;
maxa = maxa > id ? maxa : id;
cin >> a[id].x;
}
cin >> numb;
for (int i = 0; i < numb; i++)
{
int id = 0;
cin >> id;
maxb = maxb > id ? maxb : id;
cin >> b[id].x;
}
sum = maxa + maxb;
int digitnum = 1;
for (; sum > 0; sum >>= 1, digitnum++);
sum = 1;
for (; digitnum > 0; sum <<= 1, digitnum--);
Real_DFT(a, false, sum);
Real_DFT(b, false, sum);
for (int i = 0; i < sum; i++)
a[i] = a[i] * b[i];
Real_DFT(a, true, sum);
int num=0;
for (int i = 0; i <= sum; i++)
{
if (a[i].x / sum > 0.05||a[i].x/sum<-0.05)
{
num++;
is_output[i] = 1;
}
}
cout << num;
for (int i = sum; i >=0; i--)
{
if(is_output[i]==1)
cout << " " <<i<<" "<< std::fixed << setprecision(1) << (a[i].x / sum);
}
return 0;
}
输入
2 1 2.4 0 3.2
2 2 1.5 1 0.5
输出
3 3 3.6 2 6.0 1 1.6
|


